Introducción
Considerando la distribución de muestreo de un estimador: \(\overline{y}_c\): Valores posibles del estimador \(P_c\) : Probabilidad de materialización del estimador c
La media de la distribución de muestreo es el valor esperado(la esperanza matemática) del estimador:
\[\displaystyle E(\overline{y})= \sum_{c}{P_c\overline{y}_c}\]
\(\displaystyle E(\overline{y})-\overline{Y}\) : Sesgo de muestreo
Considerando si el estimador es insesgado, sucedería lo sgte para toda la distribución muestral del estimador: Si \[\displaystyle E(\overline{y})-\overline{Y}=0 \rightarrow E(\overline{y})= \overline{Y}\]
Desviación Estandar (Error Estándar): La raíz cuadrada de la varianza de la distribución de muestreo del estimador, que también es la desviación cuadrática media alrededor de la media \(E(\overline{y})\) :
\[ \displaystyle Var(\overline{y}) = \sum_{c}{P_c[y_c-E(\overline{y})]^2} \quad S(\overline{y})=\sqrt{Var(\overline{y}}) \]
Error Cuadrático Medio de la distribución de muestreo se relaciona con la varianza, pero en este las desviaciones se toman alrededor del valor \(\overline{Y}\)
\[ \displaystyle ECM(\overline{y})=\sum_{c}{P_c(\overline{y}_c-\overline{Y})^2}=Var(\overline{y})+[E(\overline{y})-\overline{Y}]^2 \]
EL termino adicional \([E(\overline{y})-\overline{Y}]^2\) es el cuadrado del sesgo de muestreo, este se anula en los diseños de muestreo insesgados. Y si no es cero, el sesgo de muestreo es pequeño para la mayoría de las muestras bien diseñadas, y tiende a disminuir conforme aumenta el tamaño de la muestra.
La inferencia estadística se base a errores estándares de la forma de intervalos:
\[ [\overline{y} \pm t_ps(\overline{y})] \]
En el Muestreo Probabilistico cada elemento dela población tiene una probabilidad conocida y no nula de ser seleccionada.
| I | Mesip (Métodos de Selección con Igual Probabilidad) para todos los elementos: a) Probabilidades iguales en todas las etapas b) Probabilidades totales iguales para todos los elementos, obtenidas compensando probabilidades desiguales en diversas etapas |
Probabilidades desiguales para elementos diferentes; compensadas generalmente con ponderaciones inversas. a) Causadas por irregularidades en los marcos y los procedimientos de selección b) Afijación o Asignación desproporcional diseñada para una asignación óptima |
| II | Muestreo de elementos: en una sola etapa, la unidad de muestreo contiene solamente un elemento | Muestreo de conglomerados: las unidades de muestreo son conglomerados de elementos a) Muestreo de conglomerados en una etapa b) Submuestreo o muestreo polietápico c) Conglomerados iguales d) Conglomerados desiguales |
| III | Selección no estratificada: las unidades de muestreo seleccionadas de la población completa | Muestreo estratificado: selecciones separadas de particiones,característica o estratos de la población. |
| IV | Selección aleatoria de unidades individuales de muestreo de estrato completo o de la población | Selección sistemática de unidades de muestreo con un intervalo de selección aplicado a una lista |
| V | Muestreo en una fase o etapa (monoetápica): La muestra final seleccionada directamente de la población completa | Muestreo de dos fases (muestreo doble) : la muestra final seleccionada de una muestra de primera fase, que obtiene información para estratificación o para estimación |
Notación
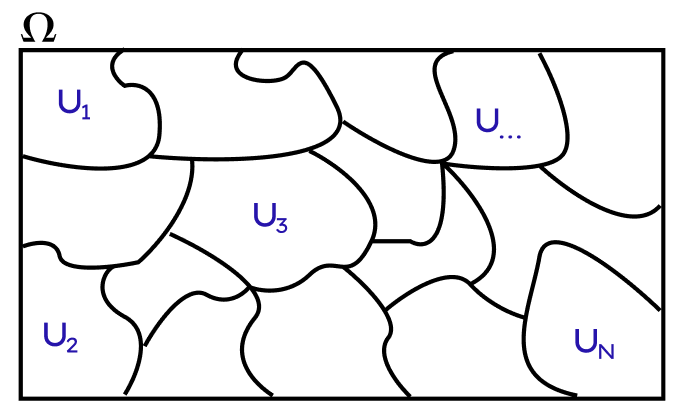
Supongamos que nuestra Población esta dada por las siguientes unidades o elementos(personas, viviendas, areas, departamentos,etc): \(U_1,\quad U_2,\quad ...,\quad U_N\) donde:
Valores de la población
\(N=\)número de elementos en la población
\(Y_i =\)valor de la variable y para el elemento i-ésimo de la población. Tambien se utiliza para denotar la variable \(y\) como elemento general
\(\displaystyle Y= \sum_{i=1}^{N}Y_i =\) total de la población para la variable \(y\). El subíndice i indica el número de listado del elemento de la población. El signo \(\displaystyle \sum_{i=1}^{N}\) indica la suma sobre todos los elementos de la población (i=1,2,….,N).
\(\displaystyle \overline{Y}=\frac{Y}{N}=\frac{1}{N} \sum_{i=1}^{N}Y_i =\) media de la población por elementos de la variable \(Y_i\)
\[\displaystyle S_y^2=\frac{1}{N-1}\sum_{i=1}^{N}{(Y_i-\overline{Y})^2} \quad \sigma_2^2=\frac{1}{N}\sum_{i=1}^{N}{(Y_i-\overline{Y})^2} \rightarrow S_y^2=\frac{N}{N-1}\sigma_y^2\]
La varianza de los elementos de la población tiene dos definiciones \(\sigma_y^2\) es más tradicional pero \(S_y^2\) simplifica muchas fórmulas. La diferencia entre las dos desaparece para poblaciones grandes.
\(S_y\) o \(\sigma_y =\) desviación estándar de los elementos de la población.
Valores de la muestra
\(y_i=\) Valor de la variable \(Y_i\) para el elemnto j-ésimo de la muestra.
\(y=\sum_{j=1}^{n}y_j =\) Total de la muestra para la variable \(Y_i\)
\(\displaystyle \overline{y}=\frac{y}{n}=\frac{1}{n} \sum_{j=1}^{n}y_i =\) Media simple de la muestra por elemento de la variable \(Y_i\). El índice \(j\) aplicable a la muestra varía de 1 a \(n\). El signo \(\sum_{j=1}^{n}\) indica la suma sobre todos los elementos de la muestra (j=1,2,…,n)
En muchos diseños de muestreo mesip, pero no en todos, se usa \(\overline{y}\) para estimar \(\overline{Y}\). En forma semejante, \(N\overline{y}\) puede usarse como estimador de \(\overline{Y}\). Nótese que \(N\overline{y}=\frac{N}{n}y=\frac{y}{f}\)
\(\displaystyle S_y^2=\frac{1}{n-1}\sum_{i=1}^{n}{(y_i-\overline{y})^2}=\) varianza de los elementos de la muestra. Es más fácil de calcular en la forma \(\displaystyle \frac{1}{n-1} [ \sum_{j=1}^ny_j^2-n\overline{y}^2]\).
Muestreo Aleatorio Simple (MAS)
Muestreo Con Reemplazo - No Restricto (c.r)
\(P(\text{Seleccionar }U_i)=\frac{1}{N}\)
Muestreo Sin Reemplazo - Irrestricto (s.r)
\(P(\text{Seleccionar }U_i\text{ en el }1^{er}\text{ sorteo})=\frac{1}{N}\)
\(P(\text{Seleccionar }U_i \wedge U_j \text{ sean seleccionados})=\frac{1}{N}\frac{1}{N-1}=P(U_j)P(U_i\mid U_j)\)
| Por el Teorema de la Probabilidad Total: |
| Sean los sucesos \(A_1,A_2,\ldots,A_n\) una partición del espacio muestral \(\Omega\), y sea \(B\) un suceso cualquiera, se cumple que la probabilidad del suceso \(B\) puede expresase en función de los sucesos \(A_i\) de la sgte manera: \(P(B)=P(B \mid A_1)\cdot P(A_1) + P(B \mid A_2)\cdot P(A_2) + \cdots +P(B \mid A_n)\cdot P(A_n)\) |
\(P(\text{Seleccionar }U_i\text{ en el }2^{do}\text{ sorteo})=\)
\(=P(U_1\cap U_j\cup U_2\cap U_j \cup \ldots \cup U_N\cap U_j)\)
\(=P(U_1\cap U_j)+ P(U_2\cap U_j)+ \ldots + P(U_N\cap U_j)\)
\(=P( U_j)P(U_1 \mid U_j)+ P( U_j)P(U_2 \mid U_j)+ \ldots + P( U_j)P(U_N \mid U_j)\)
donde \(\ldots \rightarrow P( U_j)P(U_j \mid U_j)\rightarrow P(U_j \mid U_j)=0\)
\(=\frac{1}{N}\frac{1}{N-1}+\ldots+\frac{1}{N}\frac{1}{N-1},\quad N-1 \quad veces\)
\(=\sum_{i=1}^NP(U_j)P(U_i\mid U_j)\)
\(=\sum_{i=1}^N\frac{1}{N}\frac{1}{N-1}=(N-1)\frac{1}{N}\frac{1}{N-1}=\frac{1}{N}\)
Por lo tanto: \(P(\text{Seleccionar }U_i\text{ en el }2^{do}\text{ sorteo})=\frac{1}{N}\)
\(P(\text{Seleccionar }U_i\text{ en el }3^{er}\text{ sorteo})=\frac{1}{N}\)
\(P(\text{Selección S produsca la }U_i \mid\text{ Una selección previa ha producido la } U_j, i\neq j)= \frac{1}{N-1}\)
\(P(\text{Selección R y S seleccione }U_i \text{ y } U_j) = P(U_i)P(U_j\mid U_i)+ P(U_j)P(U_i\mid U_j)=\)
\(=\frac{1}{N}\frac{1}{N-1}+\frac{1}{N}\frac{1}{N-1}=\frac{2}{N(N-1)}\)
\(P(U_i\text{ sea seleccionada de una muestra de tamaño n})=\frac{n}{N}\)
\(P(U_i \wedge U_j \text{ sean seleccionadas de una muestra de tamaño n})=P(U_j)P(U_i\mid U_j)=\frac{n}{N}\frac{n-1}{N-1}\)
\(P(\text{ Seleccionar n elementos de la población N})=\frac{1}{\binom{N}{n}}\)
| Estimadores de | Des Raj | Leslie Kish | Sharon Lohr |
|---|---|---|---|
| Media | \(\displaystyle{\hat{\overline{Y}}=\overline{y}=\frac{1}{n}S_{i=1}^{n}y_i}\) | \(\displaystyle{\overline{y}_0=\frac{1}{n}\sum_{j=1}^{n}y_j}\) | \(\displaystyle{\hat{\overline{Y}}=\overline{y}=\frac{1}{n}S_{i=1}^{n}y_i}\) |
| Varianza del estimador de la Media | \(\displaystyle{\hat{V}(\overline{y})=(1-f)\frac{s^2}{n}}\) \(s^{2}=\frac{S_{j=1}^{n}(y_j-\overline{y})^2}{n-1}\) \(f=\frac{n}{N}\) |
\(\displaystyle{var(\overline{y}_0)=(1-f)\frac{s^2}{n}}\) \(s^2=\frac{\sum_{j=1}^{n}(y_j-\overline{y})^2}{n-1}\) |
\(\displaystyle{\hat{V}(\overline{y})=(1-f)\frac{s^2}{n}}\) \(s^{2}=\frac{1}{n-1}\sum_{j=1}^{n}(y_j-\overline{y})^2\) |
| Error Estándar del estimador de la media | \(s_{\overline{y}}=\sqrt{\hat{V}(\overline{y})}\) | \(s(\overline{y})=\sqrt{var(\overline{y}_0)}\) | \(se(\overline{y})=\sqrt{\hat{V}(\overline{y})}\) |
| Error Relativo o Coeficiente de Variación del estimador de la media | \(\hat{CV}(\overline{y})=\frac{\sqrt{\hat{V}(\overline{y})}}{\overline{y}}\) | \(cv(\overline{y})=\frac{s(\overline{y})}{\overline{y}}\) | \(\hat{CV}(\overline{y})=\frac{se(\overline{y})}{\overline{y}}\) |
| Total | \(\hat{Y}=N\overline{y}\) | \(\hat{Y}=N\overline{y}\) | \(\hat{t}=N\overline{y}\) |
| Varianza del estimador del Total | \(\displaystyle{\hat{V}(\hat{Y})=N^2(1-f)\frac{s^2}{n}}\) | \(\displaystyle{\hat{V}(\hat{Y})=N^2(1-f)\frac{s^2}{n}}\) | \(\displaystyle{\hat{V}(\hat{t})=N^2(1-f)\frac{s^2}{n}}\) |
| Proporción \(Y_i=1,0\) | \(\hat{p}=\overline{y}\) | \(\hat{p}=\overline{y}\) | \(\hat{p}=\overline{y}\) |
| Varianza del estimador de la Proporción | \(\displaystyle{\hat{V}(\hat{p})=(1-f)\frac{\hat{p}(1-\hat{p})}{n-1}}\) \(=(1-f)\frac{\hat{p}\hat{q}}{n-1}\) | \(\approx\) | \(\approx\) |
| Tamaño de Muestra tomando en cuenta el estimador de la media | \(\displaystyle n>\frac{S_y^2}{(\overline{Y}a_0)^2+\frac{S_y^2}{N}}\) \(a_0=CV_{fijado}\) Y los otros valores poblacionales se toman de investigaciones pasadas |
\(\approx\) | \(\approx\) |
Tamaño de muestra, basados en la Normalidad Asintótica
Si \(n\) aumenta(es grande) se cumple lo sgte:
\[ \overline{y} \sim N(\overline{Y},\frac{\sigma^2}{n}) \]
\[ \rightarrow \overline{y} \sim N(\overline{Y},V(\overline{y})),V(\overline{y})=(1-f)\frac{S_y^2}{n} \]
\[ P(-z_{\alpha/2}<\frac{\overline{y}-\overline{Y}}{\sqrt{V(\overline{y})}}<z_{\alpha/2})=1-\alpha \] \[P(\overline{y}-z_{\alpha/2}\sqrt{V(\overline{y})} <\overline{Y}<\overline{y}+z_{\alpha/2}\sqrt{V(\overline{y})})=1-\alpha\] Definimos el margen de error como: \[e=z_{\alpha/2}\sqrt{V(\overline{y})}= \sqrt{(1-\frac{n}{N})}\frac{S_y}{\sqrt{n}}\] Del cual resolveremos la ecuación en función de \(n\), definimos a \(n_0\) como:
\[n_0=(\frac{z_{\alpha/2}S_y}{e})^2\] Para luego definir nuestro tamaño de muestra \(n\):
\[n=\frac{n_0}{1+\frac{n_0}{N}}\]
Tamaño de Muestra Tomando en consideración un nivel deseado de variación
\[\displaystyle n>\frac{S_y^2}{V_0+\frac{S_y^2}{N}} \rightarrow \frac{P(1-P)}{V_0 +\frac{P(1-P)}{N}}\] Donde \(V_0\) puede ser cualquier nivel deseado de precisión como:
- Varianza Muestral(\(V(\overline{y})\)): \(V_0=V(\overline{y})\)
- Error Estandar(\(SE(\overline{y})\)): \(V_0=SE(\overline{y})^2\)
- Coeficiente de Variación(\(CV(\overline{y})\)): \(V_0=(CV(\overline{y})*\overline{y})^2\)
- Margen de error(\(e\)): \(V_0=(\frac{e}{z_{1-\alpha/2}})^2\)
